La non-réciprocité des ondes obtenue par la modulation temporelle d’un seul paramètre physique
Le principe de réciprocité assure que les ondes transmises d’une source à un récepteur sont les mêmes si on intervertit source et récepteur. Briser cette réciprocité n’est possible que dans des milieux bien particuliers. Une stratégie connue consiste à moduler en temps les paramètres physiques du problème étudié. Une collaboration internationale a démontré que la non-réciprocité était en fait atteignable dans davantage de cas, plus faciles à mettre en œuvre. Une piste pour nombreuses expériences en acoustique et en photonique.
S’il existe différents types d’ondes, par exemple sonores ou électromagnétiques, la physique classique décrit leur comportement par des équations similaires. Les ondes sont ainsi toutes concernées par le principe de réciprocité, selon lequel un signal allant d’un point A à un point B est, à l’arrivée, identique à un même signal parti du point B jusqu’au point A. Briser la réciprocité trouve de nombreuses applications, comme dans les diodes, qui ne font passer le courant que dans un sens, ou pour l’atténuation de vibrations, en les évacuant d’un domaine sans en laisser d’autres entrer. La non-réciprocité a lieu dans trois grands cas de figure. Quand l’onde se propage dans un milieu non linéaire, c’est-à-dire qui n’affecte pas le signal de manière proportionnelle au forçage, ou dans un écoulement auquel on apporte de l’énergie. Enfin, la non-réciprocité s’obtient en modulant les paramètres physiques du milieu de propagation au cours du temps et de l’espace. Il était admis dans ce troisième cas de figure que, malgré quelques contradictions théoriques, deux paramètres devaient absolument être modifiés en simultané. Or, dans la pratique, ce n’est pas réalisable car, quels que soient le type d’onde et son milieu de propagation, il y a toujours un paramètre trop difficile, voire impossible, à moduler. Par exemple, il n’existe pas de solution pour modifier la masse volumique d’un matériau pendant qu’une onde le traverse. Des chercheurs et une chercheuse du Laboratoire de mécanique et d’acoustique (LMA, CNRS/Aix-Marseille Université/Centrale Méditerranée), de l’Imperial College de Londres (Royaume-Uni), de l’IRL Abraham de Moivre (CNRS/Imperial College London) et de l’Université de Manchester (Royaume-Uni) ont montré que la non-réciprocité est en fait possible en ne modulant qu’un seul paramètre dans le temps.
Ces travaux théoriques reposent sur la méthode d’analyse mathématique dite d’homogénéisation, qui relie le comportement global d’un matériau à la structure hétérogène. Utilisée pour étudier la non-réciprocité, l’homogénéisation est systématiquement employée, pour des raisons de simplicité, à l’ordre zéro des développements asymptotiques. Dans ce cas, réservé aux ondes de basses fréquences, la modulation simultanée de deux paramètres dans le temps et l’espace est nécessaire pour obtenir une non-réciprocité. Les scientifiques ont ici refait les calculs à l’ordre un, puis deux. Cela revient à considérer une cascade d’équations aux dérivées partielles, la solution de l’une servant de source à l’autre. Avec l’homogénéisation à l’ordre deux, des ondes de bien plus hautes fréquences peuvent être étudiées et la non-réciprocité apparaît alors possible en ne modulant qu’un seul paramètre.
Cette découverte implique que la question doit être traitée avec des calculs bien plus complexes qu’auparavant, mais elle réconcilie la théorie avec d’autres techniques d’analyse. Elle ouvre surtout la porte à un grand nombre d’expériences pour tester les effets de la modulation dans le temps d’un seul paramètre sur les ondes.
La non-réciprocité des ondes obtenue par la modulation temporelle d’un seul paramètre physique
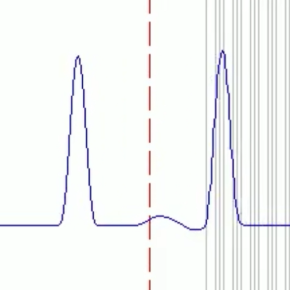
Simulation d’une onde qui traverse un réseau d’interfaces (traits gris) qui se déplace au fil du temps. Selon que l’onde aille de gauche à droite ou à l’inverse, sa forme n’est pas la même. Nous sommes donc dans une situation de non-réciprocité.
© Bruno Lombard
Audiodescription
Références
High-order homogenisation of the time-modulated wave equation: non-reciprocity for a single varying parameter.
Marie Touboul, Bruno Lombard, Raphaël Assier, Sébastien Guenneau, Richard V. Craster.
Proceedings Royal Society London A., 2024.
https://doi.org/10.1098/rspa.2023.0776